New World
[이산수학#6] 관계 본문
728x90
반응형
1. 기본사항
곱집합 : 모든 순서쌍들의 집합
𝑨 × 𝑩 = 𝒂, 𝒃 𝒂 ∈ 𝑨, 𝒃 ∈ 𝑩}
관계 : 𝒙는 𝒚와 𝑹의 관계
(𝒙, 𝒚) ∈ 𝑹 ⇒ ⇒ 𝒙𝑹𝒚로 표기
𝑿 = 𝒀이면 𝑹을 𝑿에서의 관계
2. 관계의 표현
| 화살표 도표 : 화살표를 그려 나타낸 관계 | 방향 그래프 ( G = (V, E) ) : 점과 선으로 이루어진 도형 | 방향 , 무향 , 일반 |
부울 행렬 |
 |
 |
 |
3. 관계의 성질
| 반사적 | 대칭적 | 추이적 |
| ∀𝒂 ∈ 𝑨 (𝒂, 𝒂) ∈ 𝑹 |
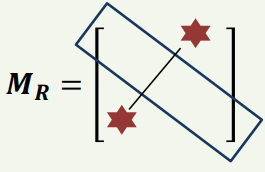
∀𝒂, 𝒃 ∈ 𝑨 𝒂, 𝒃 ∈ 𝑹 ⇒ (𝒃, 𝒂) ∈ 𝑹 |
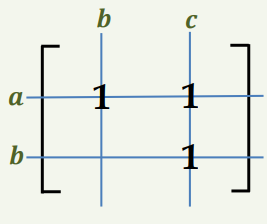
∀𝒂, 𝒃, 𝒄 ∈ 𝑨 ((𝒂, 𝒃) ∈ 𝑹 ㅅ (𝒃, 𝒄) ∈ 𝑹) ⇒ (𝒂, 𝒄) ∈ 𝑹 |
| 자신의 집합으로 다시 돌아오는 관계 | 서로가 서로에게 관계 | A -> B, B -> C => A -> C 관계 |
 |
 |
 |
4. 관계의 종류
역관계 : 현재 관계의 역으로 된 관계
𝑿, 𝒀 ∶ 집합 𝑹 ∶ 𝑿에서 𝒀로의 관계
𝑹 −𝟏 ∶ 𝑹의 역관계(inverse relation)
𝑹 −𝟏 = {(𝒚, 𝒙) | (𝒙, 𝒚) ∈ 𝑹 } ⊂ 𝒀 × 𝑿
합성관계
𝑨, 𝑩, 𝑪 ∶ 집합 𝑹 ∶ 𝑨에서 𝑩로의 관계, 𝑺 ∶ 𝑩에서 𝑪로의 관계
𝑹과 𝐒의 합성관계(composition relation)
𝑺 ∘ 𝑹 = {(𝒂, 𝒄) | 𝒂 ∈ 𝑨, 𝒃 ∈ 𝑩, 𝒄 ∈ 𝑪, (𝒂, 𝒃) ∈ 𝑹, (𝒃, 𝒄) ∈ 𝑺 }
𝑺 ∘ 𝑹 ⊂ 𝑨 × 𝑪 (𝑨에서 𝑪로의 관계)
𝑴𝑹은 𝒎 × 𝒏 부울행렬
𝑴𝑺은 𝒏 × 𝒑 부울행렬
𝑴𝑺∘𝑹은 𝒎 × 𝒑 부울행렬
=> 𝑴𝑺∘𝑹 = 𝑴𝑹⊙𝑴𝑺
동치관계 : 반사적, 대칭적, 추이적인 관계
동치류 : 동치관계에 있는 집합
𝑨 ∶ 집합
𝑹 ∶ 𝑨에서의 동치관계
𝑨의 임의의 원소 𝒂에 대해서 |𝒂| = {𝒙 ∈ 𝑨 (𝒂, 𝒙) ∈ 𝑹} 를 𝒂의 동치류
반응형
'Self-Study > Study' 카테고리의 다른 글
| [이산수학#8] 부울대수 (0) | 2022.05.06 |
|---|---|
| [이산수학#7] 함수 (0) | 2022.05.06 |
| [이산수학#4, 5] 집합론, 행렬 (0) | 2022.05.04 |
| [이산수학#3] 증명 (0) | 2022.05.04 |
| [이산수학#2] 논리 (0) | 2022.05.03 |
Comments



