New World
[이산수학#4, 5] 집합론, 행렬 본문
1. 기본사항
집합 표기법
- 원소 : 𝒂 ∈ 𝑺, 𝒃 ∉ 𝑺
- 집합 : 𝑺 = {1, 2, 3} / 𝑺 = { 𝒙|𝟎 < 𝒙 < 𝟒 인 자연수}
- 집합의 크기 : |𝑺| = 3
부분집합 : A의 모든 원소가 B의 원소라면 A는 B의 부분집합 (𝑨 ⊆ 𝑩 ⇔ ∀x 또는 𝐀 ⊂ 𝑩 )
진부분집합 : 𝑨 ⊆ 𝑩, 𝑩 ⊆ 𝑨 ⇔ 𝑨 ⊆ 𝑩, 𝑨 ≠ 𝑩
상동 : 𝑨 = 𝑩 ⇔ 𝑨 ⊆ 𝑩 𝒂𝒏𝒅 𝑩 ⊆ 𝑨
서로소 : 서로 겹치는 원소가 없는 사이
분할 : 집합을 공집합이 아닌 부분집합들로 나눌 때 그 집합의 모든 원소들이 각각 나눠진 부분집합들 중 하나에만 포함될 경우 전체 집합을 그 집합의 분할이라고 함
멱집합 : 집합의 모든 부분집합들의 집합 ( P(A) 로 표기)
2. 집합연산
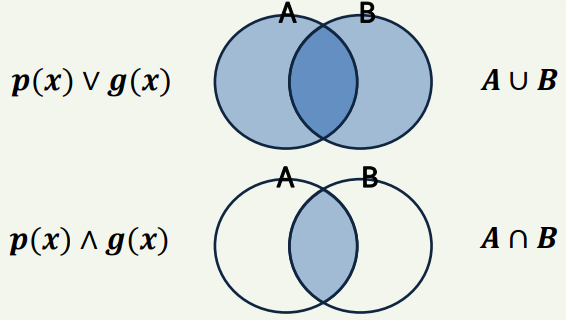
-합집합 : 전체 집합 | 𝑨 ∪ 𝑩 = {𝒙 ∈ 𝑼|𝒙 ∈ 𝑨 ∨ 𝒙 ∈ 𝑩}
-교집합 : 집합끼리 겹치는 부분집합 | 𝑨 ∩ 𝑩 = {𝒙 ∈ 𝑼|𝒙 ∈ 𝑨 ∧ 𝒙 ∈ 𝑩}
-차집합 : 집합에서 교집합을 제거한 집합 | 𝑨 − 𝑩 = {𝒙 ∈ 𝑼|𝒙 ∈ 𝑨 ∧ 𝒙 ∉ 𝑩}
-여집합 : 집합의 반전되는 영역 | 𝑨 𝒄 = 𝑼 − 𝑨 = {𝒙 ∈ 𝑼|𝒙 ∉ 𝑨}
-대칭차집합 : 합집합에서 교집합을 제거한 집합 | 𝑨⨁𝑩 = {𝒙 ∈ 𝑼|𝒙 ∈ 𝑨 ∪ 𝑩 ∧ 𝒙 ∉ 𝑨 ∩ 𝑩}
-곱집합 : 𝑨 × 𝑩 = 𝒂, 𝒃 𝒂 ∈ 𝑨, 𝒃 ∈ 𝑩 }
3. 집합의 대수법칙
1. 집합의 크기에 관한 성질
합집합의 크기 : |𝑨 ∪ 𝑩| = |𝑨| + |𝑩| − |𝑨 ∩ 𝑩|
서로소인 집합의 합집합의 크기 : |𝑨 ∪ 𝑩| = |𝑨| + |𝑩|
2. 포함관계 및 항등식
원소 논증 : ∀𝒙 ∈ 𝑿 → 𝒙 ∈ Y
집합의 항등식 : 교환법칙, 결합법칙, 분배법칙, 항등법칙, 보수법칙, 이중보수법칙, 멱등법칙, 전체 합계 법칙, 드모르간의 법칙, 홉수 법칙, 𝑼와 ∅의 여집합, 차집합법칙
1. 기본사항
행렬 : 행과 열로 구성되는 사각형 형태로 수를 배열
영행렬 : 모든 원소가 0인 행렬
2. 행렬의 연산
1. 기본연산
행렬의 합, 차, 스칼라곱
합의 연산법칙 : 교환법칙, 결합법칙, 항등원, 역원
스칼라곱 연산법칙 : 결합법칙, 분배법칙
행렬의 곱 : 𝑨(𝒎 × 𝒏 행렬)와 𝑩(𝒏 × 𝒍)의 행렬의 곱 𝑨𝑩는 𝒎 × 𝒍 행렬
2. 가우스소거법
역행렬이 존재한다면 방정식의 해를 구할 수 있음
행 교환, 행 스케일링, 행 대체 연산
행제형 행렬 : 영행이 아닌 행은 영행의 위, 첫번째 0이 아닌 원소를 선도원소
소거행제형 : 선도원소가 포함된 열에서 선도원소를 제외한 모든 원소가 0인 행제형 행렬
3. 행렬의 종류
정방행렬 : n x n 행렬을 n차 정방행렬, n을 차수, 대각 원소, 주대각선
대각행렬 : n차 정방행렬에서 대각원소 이외의 모든 원소가 0인 행렬
단위행렬 : n차 정방행렬에서 대각원소가 모두 1이고 나머지 원소는 모두 0인 행렬
대칭행렬 : 대각선을 따라 대각선을 통해 만나는 원소가 동일한 원소인 행렬
역대칭행렬 : 대칭행렬에서 음수로 동일값이 노출되며 n차 정방행렬에서 대각원소가 모두 0인 행렬
삼각행렬 : 상삼각행렬 or 하삼각행렬
상삼각행렬 : 주대각선 아래 있는 모든 원소가 0
하삼각행렬 : 주대각선 위에 있는 모든 원소가 0
전치행렬 : 행렬의 행과 열을 서로 교환한 행렬
역행렬 : 행렬이 역가능하는 것
4. 부울행렬
부울행렬 : 행렬의 모든 원소가 부울값(0, 1)으로만 구성되는 행렬
부울행렬 합 : 𝑪 = 𝑨 ∨ B , 교차 : 𝑪 = 𝑨 ∧ B , 부울곱 : 𝑪 = 𝑨⨀B
'Self-Study > Study' 카테고리의 다른 글
| [이산수학#7] 함수 (0) | 2022.05.06 |
|---|---|
| [이산수학#6] 관계 (0) | 2022.05.05 |
| [이산수학#3] 증명 (0) | 2022.05.04 |
| [이산수학#2] 논리 (0) | 2022.05.03 |
| [컴퓨터 보안#14, #15] 해시함수 및 전자서명, 공개키 기반 구조(PKI) (0) | 2022.05.03 |


