New World
[방통대] 정리집 | 이산수학 본문
728x90
반응형
| 강의 | 강의 내용 |
| 1강 | 1.1 이산수학 – 개관 1.2 모델링과 추상화 1.3 알고리즘 언어 1.4 이산수학의 응용분야 |
| 2강 | 명제 명제 : 참과 거짓을 구별할 수 있는 문장이나 수학적 식 명제 종류 : 합성명제, 조건명제, 쌍조건명제, 항진명제, 모순명제 논리연산 합성명제 : 하나 이상의 명제와 논리연산자 그리고 괄호로 이루어진 명제 논리합 : P v Q 논리곱 : P ㅅ Q 부정 : ~P 배타적 논리합 : XOR 사용, (P ㅅ~Q) v (~PㅅQ) 조건명제 : 조건의 역할을 수행하고 Q가 결론의 역할을 수행하는 경우 (비슷한 단어. 쌍조건명제) 동치 : 두 명제 p와 q가 논리적으로 동등하면 논리적 동치 술어논리 논리 : 명제 논리, 술어 논리 추론 |
| 3강 | 기본사항 공리 : 명제들을 증명하기 위해 전제로 사용되는 가장 기본적인 가정, 별도의 증명 X 참으로 이용 증명 : 특정한 공리들을 가정, 제안된 명제가 참임을 입증 정리 : 공리로부터 증명된 명제 - 보조정리 : 정리를 증명하는 과정 중에 사용되는 증명된 명제 - 따름정리 : 정리로부터 쉽게 도출되는 부가적인 명제 직접증명법 (연역법) 명제 변형 X 증명, 공리와 정의, 정리를 논리적으로 직접 연결하여 증명 수학적 귀납법 자연수 n에 대한 명제의 성질을 증명 기본단계 => 귀납가정 => 귀납단계 기본단계 : n의 출발점에서 명제가 성립하는가 확인 귀납가정 : n = k 일 때, 명제가 성립한다고 가정 귀납단계 : n = k + 1 일 때도 명제가 성립함을 증명 간접증명법 증명해야 할 명제를 증명하기 쉬운 형태로 변형하여 증명 대우증명법 : P -> Q => ~Q -> ~P 모순증명법 : P -> Q 증명 시, ~P를 가정하면 모순 발생 -귀류법 : 오류로 귀착 , 배리법 : 이치에 어긋나게 됨 반례 증명법 : 전체 한정자가 포함된 명제가 거짓임을 증명 존재 증명법 : 존재 한정자가 포함된 명제가 참임을 증명 - 구성적 존재 증명법 : 명제함수를 증명할 때 P(x)를 참으로 만드는 x를 찾거나 찾는 과정 - 비구성적 존재 증명법 : 명제함수를 증명할 때 P(x)를 참으로 만드는 x를 찾지 않고 우회적으로 명제가 타당함을 보임 다양한 증명방법 전수 증명법 : 명제에서 유도될 수 있는 경우의 수가 적을 때 일일이 모든 경우의 수를 조사 조합적 증명법 : 두 집합의 원소의 개수가 동일함을 증명 - 전단증명 : 원수가 n개인 집합 A와 원소가 m개인 집합 B를 찾은 후, 두 집합이 1:1 관계로 n = m임을 증명 - 중복산정 : 동일한 집합의 원소를 두 가지 방법으로 세어 결과가 n과 m이면 n = m임을 증명 컴퓨터 이용 증명법 : 증명하기 복잡한 경우 컴퓨터의 데이터 처리능력을 사용 ex)4색 정리 |
| 4강 & 5강 | 기본사항 집합 표기법 - 원소 : 𝒂 ∈ 𝑺, 𝒃 ∉ 𝑺 - 집합 : 𝑺 = {1, 2, 3} / 𝑺 = { 𝒙|𝟎 < 𝒙 < 𝟒 인 자연수} - 집합의 크기 : |𝑺| = 3 부분집합 : A의 모든 원소가 B의 원소라면 A는 B의 부분집합 (𝑨 ⊆ 𝑩 ⇔ ∀x 또는 𝐀 ⊂ 𝑩 ) 진부분집합 : 𝑨 ⊆ 𝑩, 𝑩 ⊆ 𝑨 ⇔ 𝑨 ⊆ 𝑩, 𝑨 ≠ 𝑩 상동 : 𝑨 = 𝑩 ⇔ 𝑨 ⊆ 𝑩 𝒂𝒏𝒅 𝑩 ⊆ 𝑨 서로소 : 서로 겹치는 원소가 없는 사이 분할 : 집합을 공집합이 아닌 부분집합들로 나눌 때 그 집합의 모든 원소들이 각각 나눠진 부분집합들 중 하나에만 포함될 경우 전체 집합을 그 집합의 분할이라고 함 멱집합 : 집합의 모든 부분집합들의 집합 ( P(A) 로 표기) 집합연산 -합집합 : 전체 집합 | 𝑨 ∪ 𝑩 = {𝒙 ∈ 𝑼|𝒙 ∈ 𝑨 ∨ 𝒙 ∈ 𝑩} -교집합 : 집합끼리 겹치는 부분집합 | 𝑨 ∩ 𝑩 = {𝒙 ∈ 𝑼|𝒙 ∈ 𝑨 ∧ 𝒙 ∈ 𝑩} -차집합 : 집합에서 교집합을 제거한 집합 | 𝑨 − 𝑩 = {𝒙 ∈ 𝑼|𝒙 ∈ 𝑨 ∧ 𝒙 ∉ 𝑩} -여집합 : 집합의 반전되는 영역 | 𝑨 𝒄 = 𝑼 − 𝑨 = {𝒙 ∈ 𝑼|𝒙 ∉ 𝑨} -대칭차집합 : 합집합에서 교집합을 제거한 집합 | 𝑨⨁𝑩 = {𝒙 ∈ 𝑼|𝒙 ∈ 𝑨 ∪ 𝑩 ∧ 𝒙 ∉ 𝑨 ∩ 𝑩} -곱집합 : 𝑨 × 𝑩 = 𝒂, 𝒃 𝒂 ∈ 𝑨, 𝒃 ∈ 𝑩 } 집합의 대수법칙 1. 집합의 크기에 관한 성질 합집합의 크기 : |𝑨 ∪ 𝑩| = |𝑨| + |𝑩| − |𝑨 ∩ 𝑩| 서로소인 집합의 합집합의 크기 : |𝑨 ∪ 𝑩| = |𝑨| + |𝑩| 2. 포함관계 및 항등식 원소 논증 : ∀𝒙 ∈ 𝑿 → 𝒙 ∈ Y 집합의 항등식 : 교환법칙, 결합법칙, 분배법칙, 항등법칙, 보수법칙, 이중보수법칙, 멱등법칙, 전체 합계 법칙, 드모르간의 법칙, 홉수 법칙, 𝑼와 ∅의 여집합, 차집합법칙 |
| 기본사항 행렬 : 행과 열로 구성되는 사각형 형태로 수를 배열 영행렬 : 모든 원소가 0인 행렬 행렬의 연산 1. 기본연산 행렬의 합, 차, 스칼라곱 합의 연산법칙 : 교환법칙, 결합법칙, 항등원, 역원 스칼라곱 연산법칙 : 결합법칙, 분배법칙 행렬의 곱 : 𝑨(𝒎 × 𝒏 행렬)와 𝑩(𝒏 × 𝒍)의 행렬의 곱 𝑨𝑩는 𝒎 × 𝒍 행렬 2. 가우스소거법 역행렬이 존재한다면 방정식의 해를 구할 수 있음 행 교환, 행 스케일링, 행 대체 연산 행제형 행렬 : 영행이 아닌 행은 영행의 위, 첫번째 0이 아닌 원소를 선도원소 소거행제형 : 선도원소가 포함된 열에서 선도원소를 제외한 모든 원소가 0인 행제형 행렬 행렬의 종류 정방행렬 : n x n 행렬을 n차 정방행렬, n을 차수, 대각 원소, 주대각선 대각행렬 : n차 정방행렬에서 대각원소 이외의 모든 원소가 0인 행렬 단위행렬 : n차 정방행렬에서 대각원소가 모두 1이고 나머지 원소는 모두 0인 행렬 대칭행렬 : 대각선을 따라 대각선을 통해 만나는 원소가 동일한 원소인 행렬 역대칭행렬 : 대칭행렬에서 음수로 동일값이 노출되며 n차 정방행렬에서 대각원소가 모두 0인 행렬 삼각행렬 : 상삼각행렬 or 하삼각행렬 상삼각행렬 : 주대각선 아래 있는 모든 원소가 0 하삼각행렬 : 주대각선 위에 있는 모든 원소가 0 전치행렬 : 행렬의 행과 열을 서로 교환한 행렬 역행렬 : 행렬이 역가능하는 것 부울행렬 부울행렬 : 행렬의 모든 원소가 부울값(0, 1)으로만 구성되는 행렬 부울행렬 합 : 𝑪 = 𝑨 ∨ B , 교차 : 𝑪 = 𝑨 ∧ B , 부울곱 : 𝑪 = 𝑨⨀B |
|
| 6강 | 기본사항 곱집합 : 모든 순서쌍들의 집합 𝑨 × 𝑩 = 𝒂, 𝒃 𝒂 ∈ 𝑨, 𝒃 ∈ 𝑩} 관계 : 𝒙는 𝒚와 𝑹의 관계 (𝒙, 𝒚) ∈ 𝑹 ⇒ ⇒ 𝒙𝑹𝒚로 표기 𝑿 = 𝒀이면 𝑹을 𝑿에서의 관계 2. 관계의 표현 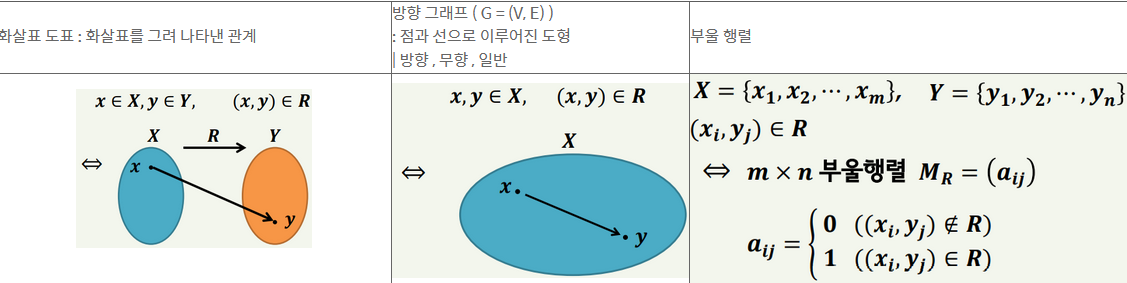 3. 관계의 성질 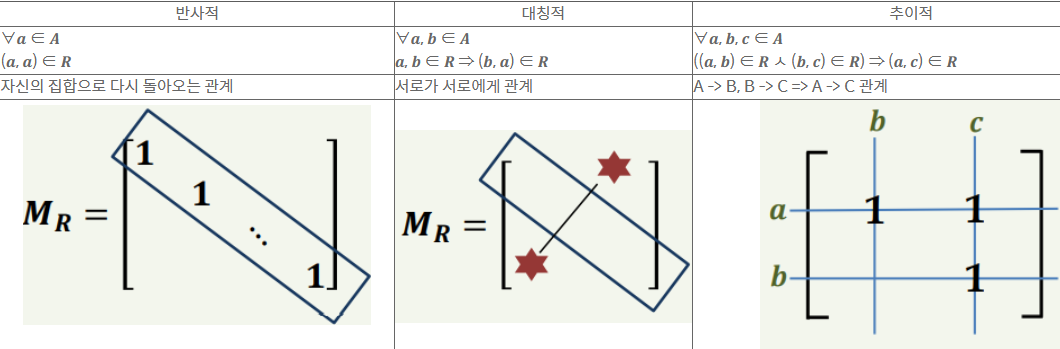 관계의 종류 역관계 : 현재 관계의 역으로 된 관계 𝑿, 𝒀 ∶ 집합 𝑹 ∶ 𝑿에서 𝒀로의 관계 𝑹 −𝟏 ∶ 𝑹의 역관계(inverse relation) 𝑹 −𝟏 = {(𝒚, 𝒙) | (𝒙, 𝒚) ∈ 𝑹 } ⊂ 𝒀 × 𝑿 합성관계 𝑨, 𝑩, 𝑪 ∶ 집합 𝑹 ∶ 𝑨에서 𝑩로의 관계, 𝑺 ∶ 𝑩에서 𝑪로의 관계 𝑹과 𝐒의 합성관계(composition relation) 𝑺 ∘ 𝑹 = {(𝒂, 𝒄) | 𝒂 ∈ 𝑨, 𝒃 ∈ 𝑩, 𝒄 ∈ 𝑪, (𝒂, 𝒃) ∈ 𝑹, (𝒃, 𝒄) ∈ 𝑺 } 𝑺 ∘ 𝑹 ⊂ 𝑨 × 𝑪 (𝑨에서 𝑪로의 관계) 𝑴𝑹은 𝒎 × 𝒏 부울행렬 𝑴𝑺은 𝒏 × 𝒑 부울행렬 𝑴𝑺∘𝑹은 𝒎 × 𝒑 부울행렬 => 𝑴𝑺∘𝑹 = 𝑴𝑹⊙𝑴𝑺 동치관계 : 반사적, 대칭적, 추이적인 관계 동치류 : 동치관계에 있는 집합 𝑨 ∶ 집합 𝑹 ∶ 𝑨에서의 동치관계 𝑨의 임의의 원소 𝒂에 대해서 |𝒂| = {𝒙 ∈ 𝑨 (𝒂, 𝒙) ∈ 𝑹} 를 𝒂의 동치류 |
| 7강 | 기본사항 X, Y : 집합 X에서 Y로의 함수 : ∀𝒙 ∈ 𝑿, ∃! 𝒚 ∈ 𝒀, 𝒙, 𝒚 ∈ 𝒇 를 만족하는 𝑿에서 𝒀로의 관계 [ 𝒇 ⊂ 𝑿 × 𝒀 ] X : f의 정의역, Y : f의 공역 y : x의 상 f(x), x : y의 역상 f(x) : f의 치역 상수함수 : 𝒇 ∶ 𝑿 → 𝒀, ∀𝒙 ∈ 𝑿, 𝒇 (𝒙) = 𝒄 (𝒄는 상수) 항등함수 : 𝒇 ∶ 𝑿 → 𝑿, ∀𝒙 ∈ 𝑿, 𝒇 (𝒙) = 𝒙 전사함수, 단사함수, 역함수  역함수 : 전단사함수인 경우 역관계의 함수 함수의 종류 계승함수 : 바닥함수 : 실수 x에 대해 x보다 작거나 같으면서 가장 큰 정수를 구하는 함수 |𝒙| = 𝒎𝒂𝒙 {𝒎 ∈ ℤ | 𝒎 ≤ 𝒙 } 천장함수 : 실수 x에 대해 x보다 크거나 같으면서 가장 작은 정수를 구하는 함수 |𝒙| = 𝒎𝒊𝒏 {𝒏 ∈ ℤ | 𝒙 ≤ 𝒏 } 나머지 함수 : 정수 n과 양의 정수 m에 대해 n을 m으로 나눴을때 나머지를 구하는 함수 |
| 8강 | 기본사항 디지털 논리회로 : 디지털 신호로 입력하여 논리연산을 통해 디지털 신호로 출력 AND 게이트 : 논리곱, F = X· Y OR 게이트 : 논리합, F = X + Y NOT 게이트 : 논리부정, F = X' NAND 게이트 : F = 𝑿' + 𝒀' NOR 게이트 : F = X'· Y' XOR 게이트 : 배타적 논리합, F = 𝑿'𝒀 + 𝑿𝒀' XNOR 게이트 : F = 𝑿'𝒀' + 𝑿𝒀 부울대수 항등법칙 : 같은 값, 𝑿 + 𝟎 = 𝑿 | 𝑿 ∙ 𝟏 = 𝑿 지배법칙 : 더해지거나 곱해지는 값과 같은 값, 𝑿 + 𝟏 = 𝟏 | 𝑿 ∙ 𝟎 = 𝟎 멱등법칙 : 같은 값을 더하거나 곱하면 나오는 값이 더하거나 곱한 값과 동일, 𝑿 + 𝑿 = 𝑿 | 𝑿 ∙ 𝑿 = 𝑿 부정법칙 : 부정하는 값을 통해 나오는 값들, 𝑿 + 𝑿' = 1 | 𝑿 ∙ 𝑿' = 𝟎 | 𝑿' = 𝑿 교환법칙 : 앞항과 뒷항의 값이 같은 값, 𝑿 + 𝒀 = 𝒀 + 𝑿 | 𝑿 ∙ 𝒀 = 𝒀 ∙ 𝑿 결합법칙 : 결합하여도 나오는 값이 동일, 𝑿 + 𝒀 + 𝒁 = 𝑿 + 𝒀 + 𝒁 | 𝑿 ∙ (𝒀 ∙ 𝒁) = (𝑿 ∙ 𝒀) ∙ 𝒁 분배법칙 : 나누어도 나오는 값이 동일, 𝑿 ∙ 𝒀 + 𝒁 = 𝑿 ∙ 𝒀 + 𝑿 ∙ 𝒁 | 𝑿 + 𝒀 ∙ 𝒁 = (𝑿 + 𝒀) ∙ (𝑿 + 𝒁) 드모르간 법칙 : (𝑿 + 𝒀)' = 𝑿'∙ 𝒀' | (𝑿 ∙ 𝒀)' = 𝑿' + 𝒀' 흡수 법칙 : 값이 흡수되는 값, 𝑿 + 𝑿 ∙ 𝒀 = 𝑿 | 𝑿 ∙ (𝑿 + 𝒀) = 𝑿 쌍대성 원리 : 부울식에서 논리곱과 논리합을 서로 바꾸고 논리 상수를 서로 바꾸면 원래 부울식의 쌍대 부울함수의 보수 -드모르간 법칙 -쌍대성 원리 이용 (F의 쌍대, F의 쌍대에서 정상형과 보수형을 서로 바꿈) 부울함수의 대수적 간소화 항결합 : 두개의 항을 결합하여 하나의 항으로 만드는 방법 문자소거 : 중복된 문자를 제거 중복항 첨가 : 부울함수의 진리값이 변하지 않도록 하면서 간소화를 위한 적절한 항을 첨가 |
| 9강 & 10강 | 기본사항 그래프는 꼭지점과 변으로 구성 병렬변 : 두 꼭지점을 연결하는 변이 복수개 루프 : 동일한 꼭지점을 연결하는 변 고립된 꼭지점 : 어떠한 변도 연결 X 꼭지점 동형 : 꼭지점과 변의 이름을 제외하고는 모두 동일한 그래프 방향 그래프 : 변이 방향을 가지는 그래프 무향 그래프 : 변이 방향이 없는 그래프 단순 그래프 : 루프와 병렬 변을 가지지 않는 무향 그래프 𝑮 = 𝑽, 𝑬 , 𝑯 = (𝑽 ′ , 𝑬′) (1) 𝑽 ′ ⊆ 𝑽, 𝑬 ′ ⊆ 𝑬 ⇒ 𝑯를 𝑮의 부분 그래프(subgraph) (2) 𝑽 ′ = 𝑽, 𝑬 ′ ⊆ 𝑬 ⇒ 𝑯를 𝑮의 신장 부분 그래프 (spanning subgraph) 총 차수 : 인접한 변의 개수 진입차수 : 들어오는 변의 개수 진출차수 : 나가는 변의 개수 path ⊂ trail ⊂ walk 워크 : 꼭지점과 변들을 순서대로 나열 트레일 : 변들이 서로 다른 것 경로 : 꼭지점이 모두 다른 것 그래프 종류 완전 그래프 : 임의의 두 꼭지점을 연결하는 변이 항상 존재 이분 그래프 : 연결 성분이 분할되어 모든 변들이 꼭지점을 인접시키는 경우 완전 이분 그래프 : 완전한 이분 그래프 k-정규 그래프 : 모든 꼭지점들이 동일한 수의 인접한 꼭지점을 갖는 그래프 그래프 표현 발생 행렬 : 꼭지점을 행으로 변을 열로 하여 발생관계를 표현 인접 행렬 : 꼭지점을 행과 열로 하여 꼭지점과 꼭지점 사이의 인접관계를 표현 인접 리스트 : 각 꼭지점에 인접하는 꼭지점들을 차례로 연결 리스트로 표현 |
| 그래프의 탐색 평면그래프 : 모든 변을 서로 교차하지 않게 그릴 수 있는 그래프 (정규, 완전 그래프) ex) 오일러의 공식, 4색 정리 오일러 투어 : 모든 변들을 각각 한번만 지나는 트레일 - 연결 그래프가 오일러 투어를 가지기 위해서는 모든 꼭지점의 차수는 짝수 해밀턴 경로 : 모든 꼭지점들을 한번씩만 지나는 경로 그래프의 활용 가중 그래프 : 그래프의 각 변에 실수값(가중치)이 붙여진 그래프 ex) 최단 경로 문제, 최소 신장 트리 문제 |
|
| 11강 | 기본사항 트리 : 사이클이 없는 단순 연결 그래프 Trivial Tree : 꼭지점 하나로 구성된 트리 Empty Tree : 꼭지점이 하나도 없는 트리 Forest : 한 개 이상의 트리로 구성된 트리 루트 트리 : 루트라 부르는 노드가 존재하며 나머지 노드들이 서로 분리된 집합으로 나뉘는 트리 트리 -> 루트 트리 (서브트리, 루트 노드) 이진 트리 공집합이거나 모든 노드가 최대 2개의 서브트리를 갖는 루트 노드인 트리 완전 이진 트리 : 왼쪽 노드부터 차례로 채워진 이진트리 - 같은 노드 수를 갖는 트리 중 최소 높이 -n개의 노드를 갖는 이진 트리의 최소 높이 : 𝑯𝒎𝒊𝒏 = |𝒍𝒐𝒈𝟐n| 포화 이진트리 : 모든 노드가 채워진 이진 트리 이진 탐색 트리 정의 : 모든 노드가 탐색을 위한 키값을 가지며 왼쪽 서브트리의 키값들은 해당 키값보다 작아야 한다 검색: 1. 루트 노드로 설정 2. 주어진 키를 비교 -일치 : 키 반환, 탐색 멈추기 -노드보다 작으면 : 왼쪽 자식을 탐색 노드로 설정, 왼쪽이 없을 경우 키 없음을 반환하며 탐색 멈추기 -노드보다 크면 : 오른쪽 자식을 탐색 노드로 설정, 오른쪽이 없을 경우 키 없음을 반환하며 탐색 멈추기 3. 2번 과정을 반복 트리의 활용 신장 트리 : 그래프의 모든 꼭지점을 포함하는 트리 최소 신장 트리 : 모든 변의 가중치 합을 총 가중치라 할 때, 가장 작은 신장 트리 Kruskal 알고리즘 1. 가중치의 오름차순으로 변을 정렬 2.가장 작은 변부터 차례대로 트리에 추가 3. 모든 꼭지점이 연결될 때까지 2반복 Prim 알고리즘 1. 꼭지점 하나를 트리에 추가 2. 트리와 연결된 꼭지점 중 가장 작은 가중치의 변으로 연결된 꼭지점을 추가 3. 2번 과정 반복 |
| 12강 | 기본 계수 법칙 두 사건 A, B가 일어날 경우의 수가 각각 N(A) = m, N(B) = n일 때, 곱의 법칙 : A, B가 동시에 일어날 경우의 수는 m x n 합의 법칙 : 𝑨 ∩ 𝑩 = ∅일때, A 또는 B가 일어날 경우의 수는 m + n 합집합의 크기 - 유한집합 |𝑨 ∪ 𝑩| = |𝑨| + |𝑩| − |𝑨 ∩ 𝑩| |𝑨 ∪ 𝑩 ∪ 𝑪| = |𝑨| + |𝑩| + |𝑪| − |𝑨 ∩ 𝑩| − |𝑨 ∩ 𝑪| − |𝑩 ∩ 𝑪| + |𝑨 ∩ 𝑩 ∩ 𝑪| - 유한집합 + 서로소 |𝑨 ∪ 𝑩| = |𝑨| + |𝑩| 순열 순열, 중복순열, 원순열 조합 𝟎 ≤ 𝒓 ≤ 𝒏을 만족하는 정수 𝒓, 𝒏 에 대하여, 𝒏개의 원소를 갖는 집합에서 𝒓 개의 원소를 순서 없이 뽑는 경우의 수 이산확률 표본공간: 실험의 모든 결과의 집합 사건: 표본공간의 부분집합 수학적 확률 : 표본공간 𝑺가 유한하며 각 사건이 발생할 가능성이 모두 동일 하다고 가정할 때 사건 𝑬(⊂ 𝑺) 가 발생할 확률 조건부 확률 : 표본공간 𝑺에 두 사건 𝑨, 𝑩가 있고, 𝑷 𝑩 > 𝟎이라고 하자. 사건 𝑩가 발생했다는 가정하에 사건 𝑨가 발생할 확률 점화식 점화식 : 수열의 항 사이에서 성립하는 관계식 비둘기집 원리 |
| 13강 | 나눗셈 a, b가 정수, a가 0이 아닐 때, b=ac 를 만족시키는 정수 c가 있다면 a가 b를 나머지 없이 나눈다 => a는 b의 약수(인수), 배수는 a|b로 표현 최대공약수 : d = gcd(a, b)로 표현, 0이 아닌 두 정수 a,b에 대해 d|a, d|b인 최대의 양의 정수 d를 a와 b의 최대 공약수 gcd(a,b) = 1인 경우, a,b는 서로소 베주의 항등식 : 적어도 하나는 0이 아닌 두 정수 a,b가 gcd(a, b) = d라 할 때, ax + by = d를 만족하는 정수 x, y 존재 - a,b가 서로소 => gcd(a,b) = 1 => ∃𝒙, 𝒚 ∈ 𝒁, 𝒂𝒙 + 𝒃𝒚 = 1 유클리드 호제법(알고리즘) - 2개의 자연수 또는 정식의 최대공약수를 구하는 알고리즘 - 두수가 서로 상대방 수를 나눠 원하는 수를 얻는 알고리즘 - a,b,q,r 가 정수면, a = bq + r이면 gcd(a,b)=gcd(b,r) 나머지 연산 나머지 함수 : 정수 n과 양의 정수 m에 대해 n을 m으로 나눴을 때 나머지를 구하는 함수, n mod m으로 표기 모듈로 합동 : a, b가 정수 m이 양의 정수면, a-b가 m으로 나눠떨어지면 a와 b는 모듈로-m 합동, a = b(mod m)으로 표기 a mod m = b mod m이 필요충분조건 소수와 소인수분해 소수 :1보다 큰 자연수 p는 p의 양의 인수가 1과 p뿐일 때 합성수 :1보다 크면서 소수가 아닌 자연수 소인수 : 주어진 자연수의 약수 중에서 소수인 것 소인수분해 : 합성수를 소인수들의 곱으로 표현 소수 판별법 - 만약 n이 합성수라면, n의 소인수 중 하나는 루트n보다 같거나 작다 가장 큰 소수 찾기 - 𝟐^𝒑 − 𝟏 (단, 𝒑는 소수 | 합성수일 경우 소수가 아님) 소수 정리 RSA 암호 |
| 14강 | 오토마타 자동장치, 스스로 움직이는 기계 ex) 컴퓨터 : 유한상태 오토마타 튜링머신 : 인간 사고과정을 구현하는 오토마타, 컴퓨터의 수학적 모델 형식언어 : 프로그래밍 언어들의 일반적인 특성들을 추상화 형식문법 : 프로그래밍 언어의 생성 규칙을 추상화 유한 오토마타 마르코프 연쇄 마르코프 성질을 지닌 이산확률과정 - 유한 오토마타의 특수한 형태 - 시간에 따른 상태의 변화를 확률로 표현 이산확률과정 - 𝑿n : 확률변수 - (𝑿𝟏,𝑿𝟐, … ,𝑿𝒏, … ) : 이산학률과정, 이산적인 시간 흐름에서 순차적으로 관측되는 확률변수의 모임 마르코프 성질 : 무기억성, 미래 상태는 오직 현재 상태에만 영향을 받는다는 성질 정상 마르코프 연쇄 : 전이 확률의 불변성, 시간의 변화에 무관하다는 성질 전이확률 : 상태 집합에서 현재 상태에서 다음 상태로 전이될 확률 표현방법 : 전이확률행렬, 상태전이도 전이확률행렬 : 행렬을 나타내는 것, 𝑷 = (𝑷𝒊𝒋) 상태전이도 : 상태와 상태전이확률을 도식화, 유한 오토마타를 표현하는 상태그래프와 기본적으로 동일 n단계 전이확률 : 채프만 콜모고로프 방정식, 페이지랭크 채프만 콜모고로프 방정식 : 현재 [𝒕 = 𝒎]상태 i 에서 n 단계 이후 [𝒕 = 𝒎 + 𝒏] 에 상태가 j 가 될 확률 페이지 랭크 : 페이지에 방문학 확률 형식 언어와 형식 문법 형식언어 : 유한한 기호들의 집합을 이용해 만들어지는 문자열의 집합 ex) 알파벳과 문자열, 언어의 연산 형식문법 : 형식 언어의 문자열들을 생성해 낼 수 있는 유한개의 규칙 ex)구구조 문법, 유도 Chomsky 계층 무제약 문법 : 제 0 유형, 생성 규칙이 𝜶 → 𝜷, 단 𝜶 ∈ (𝑽 ∪ 𝑻) + ,𝜷 ∈ (𝑽 ∪ 𝑻) ∗ 문맥 의존 문법 : 제1유형, 𝜶 → 𝜷, 단 𝜶,𝜷 ∈ (𝑽 ∪ 𝑻) + , |𝜶| ≤ |𝜷|, 생성의 우변이 좌변보다 길이가 작을 수 X 문맥 자유 문법 : 제2유형, 𝑨 → 𝜷, 단 𝑨 ∈ 𝑽, 𝜷 ∈ (𝑽 ∪ 𝑻) ∗ 정규 문법 : 제3유형, 𝑨 → 𝜶 혹은 𝑨 → 𝜶𝑩, 단 𝑨, 𝑩 ∈ 𝑽, 𝜶 ∈ 𝑻 ∗ ex) 우선형 문법, 좌선형 문법 |
반응형
'Self-Study > Study' 카테고리의 다른 글
| [방통대] 정리집 | 디지털논리회로 (0) | 2022.05.27 |
|---|---|
| [방통대] 정리집 | 데이터베이스시스템 (0) | 2022.05.27 |
| [방통대] 정리집 | 컴퓨터 보안 (0) | 2022.05.25 |
| [디지털논리회로#14, 15] 기억장치와 PLD (0) | 2022.05.22 |
| [디지털논리회로#12, 13] 레지스터와 카운터 (0) | 2022.05.22 |
Comments


