New World
[디지털논리회로#6,7,8]조합논리회로 본문
디지털논리회로 : 2 종류 (조합논리회로, 순서논리회로)
| 조합논리회로 | 순서논리회로 |
| 현재의 입력에 의해서만 출력이 결정되는 논리회로 | 조합논리회로 + 저장요소, 저장요소의 상태와 입력변수에 의해 출력이 결정 |
  |
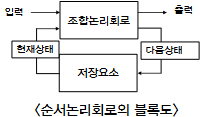 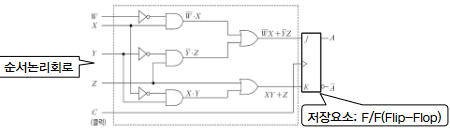 |
1. 조합논리회로의 분석과 설계
분석 : 논리회로도 -> 출력부울함수, 진리표
- 논리회로에 대해 입출력 관계를 구하는 것
- 진리표나 부울함수 유도
| 진리표 | 부울함수 |
 |
 |
 |
 |
설계 : 논리회로도 <- 출력부울함수, 진리표
- 문제에 대한 설명으로 논리회로도나 논리회로를 작성할 수 있는 부울함수 구하는 과정

2. 기본 연산회로
가산기 : 덧셈
- 2진수의 덧셈을 수행하는 조합논리회로
| 반산기(HA) : 2비트의 덧셈 | 전가산기(FA) : 3비트의 덧셈 | ||
 |
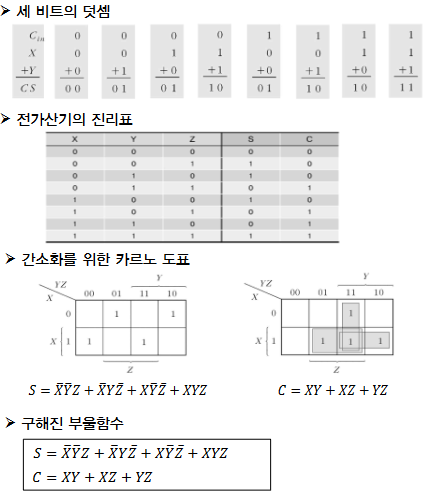 |
||
 |
 |
||
| 직/병렬 가산기 : n 비트로 된 2진수의 가산(전가산기를 이용해 구현) | |||
| 직렬 가산기 : 직렬, 회로구성비 저렴, 연산속도 늦음 | 병렬 가산기 : 병렬, 연산속도 빠름 | ||
 |
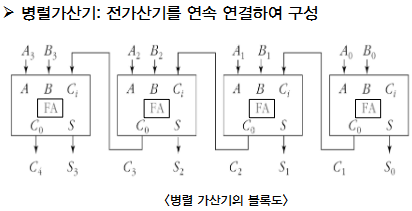 |
||
감산기 : 뺄셈
- 2진수의 뺄셈을 수행하는 조합논리회로
| 반감산기(HA) : 2비트의 뺄셈 | 전감산기(FA) : 3비트의 뺄셈 |
 |
 |
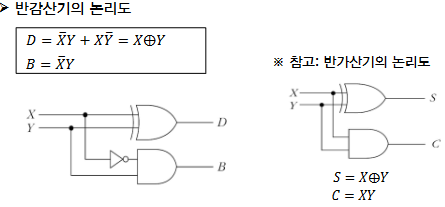 |
 |
병렬 가/감산기
2진 감산 : 가산기를 사용하여 수행, 가산기만을 사용하여 전체 회로를 최소화
A-B 감산 : B의 2의 보수를 취해 A에 더함
- 2의 보수는 1의 보수를 취한 값의 최소 유효비트에 1을 더함
- 회로에서 1의 보수는 인버터를 이용, 가산기에 입력 올림수를 1로 하면 합의 값에 1을 더하여 2의 보수가 구해짐
| 4비트 병렬 감산기 | |
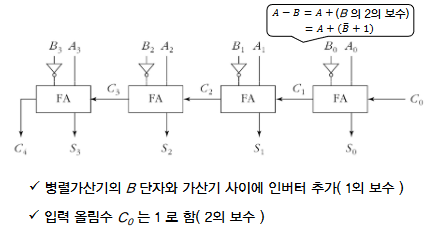 |
 |
승산기 : 곱셈
제산기 : 나눗셈
여러가지 조합논리회로 - 코드 변환기-
코드 변환기
- 하나의 2진 코드를 다른 2진 코드로 바꾸는 조합논리회로
- 디지털 시스템, 시스템들이 교환할 정보에 대해 서로 다른 코드를 사용하면 코드 변환이 필요
- 다양한 코드변환기 존재, BCD-3 초과 코드 변환기 / BCD-9의 보수 변환기
| BCD-3 초과 코드 변환기 | BCD-9의 보수 변환기 |
| BCD 코드 -> 3-초과 코드 변환기 4비트를 이용해 10진수 표현 변환회로는 4개의 입출력 필요 |
BCD 코드 -> 9의 보수값 변환 |
 |
 |
 |
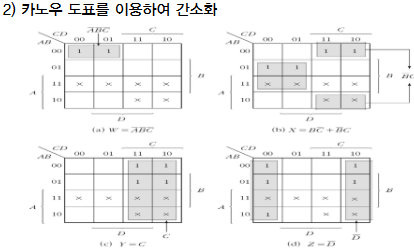 |
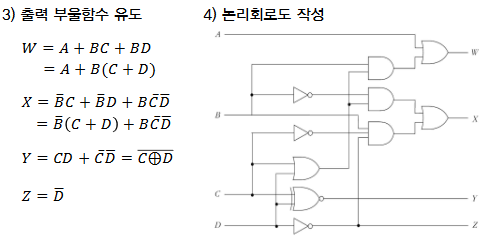 |
 |
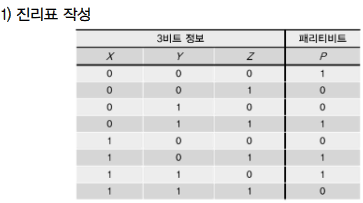
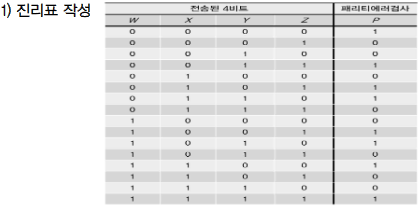
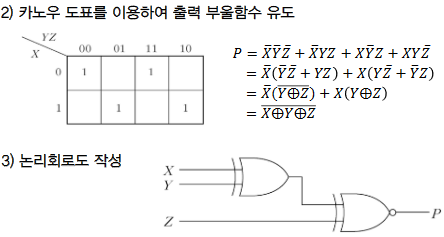
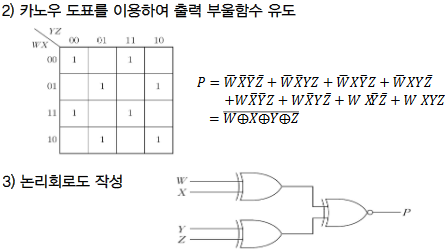
여러가지 조합논리회로 - 패리티 발생기/검사기-
- 2진 정보를 주고받을때 잡음이나 회로상의 문제로 에러 발생
- 에러 검출을 위해 전송되는 정보에 에러 검출용 비트(패리티 비트)를 추가해 전송
패리티 비트 이용 방식
짝수 패리티 검출 : 2진 정보 속에 1의 개수가 패리티 비트를 포함해 짝수
홀수 패리티 검출 : 2진 정보 속에 1의 개수가 패리티 비트를 포함해 홀수
| 이중 패리티 검출방식 | 패리티 발생기 | 패리티 검사기 |
| - 일반 패리티 검출 방식은 1개의 에러가 있을때 검출 (2개의 에러, 검출 불가) - 코드를 한 묶음으로 수직/수평방향 |
- 에러 검출이나 정정을 위해 송신측에서 전송정보에 패리티 비트를 부가, 패리티 비트를 생성하는 회로 | - 수신측에서 송신된 정보의 에러를 검출하기 위해 패리티를 검사하는 회로 |
 |
 |
 |
 |
 |
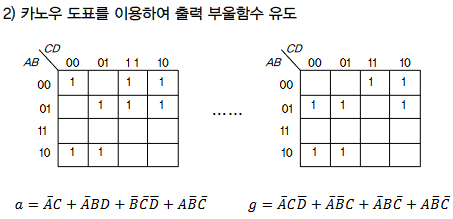
여러가지 조합논리회로 -BCD-세븐 세그먼트 표시기-
-BCD-세븐 세그먼트 표시기
세븐 세그먼트를 이용하여 BCD코드의 10진 표시를 나타내는 장치
- 표시장치의 숫자는 a, b, c, d, e, f, g 의 7개의 세그먼트로 구성
| 정의 | 설계 예 |
 |
 |
 |
|
 |
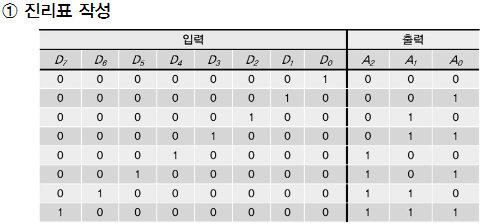
여러가지 조합논리회로 -인코더-
- 집적회로(IC)를 사용, 패키지화된 IC의 내부 게이트를 이용하면 경제적인 설계 가능
- 이미 만들어진 MSI(Medium Scale Integrated circuits)장치를 이용하면 다양한 조합논리회로의 설계가 가능
- 디지털, 효과적인 조합논리회로를 설계하기 위해서는 주어진 함수를 실현하는데 필요한 게이트의 수를 최소화할 필요
MSI장치의 예
- 인코더, 디코더, 멀티플렉서, 디멀티플렉서
인코더 : 부호화되지 않은 입력을 받아서 부호화된 출력을 내보내는 부호화기
| 정의 | 설계 예 |
 |
 |
 |

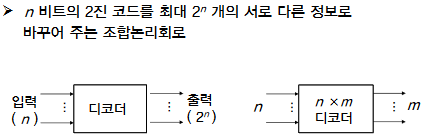
여러가지 조합논리회로 -디코더-
디코더: 부호화된 입력을 받아서 부호화되지 않는 출력을 내보내는 복호화기
| 정의 | 설계 예 |
 |
 |
 |
| 디코더의 확장 : 작은 디코더를 여러 개 결합하여 필요한 크기의 디코더 구성 |
 |
| 디코더 - n 개의 입력변수에 대한 2^n 개의 최소항을 만든다. - 부울함수는 최소항의 합으로 표현되므로, 디코더를 이용하면 부울함수를 구현할 수 있다. 결국 - n 개의 입력과 m 개의 출력을 가진 조합논리회로는 n×2^n 디코더와 m 개의 OR 게이트로 만들 수 있다. |
   |
| 멀티플렉서 | 데이터 선택기(data selector, MUX 로 표현) - 여러 개의 입력선 중에서 하나를 선택하여 단일의 출력을 내보내는 조합논리회로 - 특정 입력선을 선택하기 위해서 선택변수를 사용 - 2^n 개의 입력선 중에서 특정 입력선을 선택하기 위해서는 n 개의 선택변수의 조합에 의해 특정 입력선이 선택 |
디멀티플렉서(demultiplexer) | 데이터 분배기(data distributor, DEMUX로 표현) - 멀티플렉서와 반대되는 연산을 수행하는 조합논리회로 - 한 개의 입력선으로 부터 정보를 받아 이를 2^n 개의 출력선 중의 하나로 내보낸다. 이때 특정 출력선의 제어는 n 개의 선택입력의 조합으로 제어된다. |
 |
정답 : 2 |
 |
정답 : 3 |
 |
정답 : 3 |
'Self-Study > Study' 카테고리의 다른 글
| [디지털논리회로#12, 13] 레지스터와 카운터 (0) | 2022.05.22 |
|---|---|
| [디지털논리회로#9,10,11]순서논리회로 (0) | 2022.05.22 |
| [디지털논리회로#4,5]부울함수의 간소화 및 구현 (0) | 2022.05.21 |
| [디지털논리회로#2,3]논리게이트와 부울대수 (0) | 2022.05.21 |
| [디지털논리회로#1]디지털 논리회로와 데이터표현 (0) | 2022.05.21 |




