New World
[디지털논리회로#4,5]부울함수의 간소화 및 구현 본문
1. 간소화 방법
대수적인 방법
- 대수적으로 적용하여 간소화
- 도표방법과 테이블 방법의 이론적 바탕
도표 방법
- 카르노 도표 사용, 부울함수의 각 항들을 곱이나 합 형태로 간소화
- 6개 변수를 가진 부울함수에 사용
테이블 방법
- 퀸-맥클러스키 방법, 테이블을 사용하여 간소화 알고리즘을 구현
- 많은 변수를 가진 부울함수에 적합
1. 카르노도표 방법의 개요
카르노 도표 : 여러개의 사각형으로 된 다이어그램
- 사각형 : 각각 하나의 최소항 또는 최대항
- 도표 내의 면적을 이용해 간소화 (정규형 부울함수 => 표준형 부울 함수)
- 간소화 형태 : 최소항의 합이 곱의 합, 최대항의 곱이 합의 곱 형태
- 부울함수의 입력변수의 수에 다라 기본 도표의 형태가 결정
- 입력변수의 수가 n인 경우, n 변수 카르노 도표라함 (사각형 : 2^n개)
| 간소화 방법 | |||
 |
 |
 |
 |
2. 2, 3, 4변수 카르노 도표
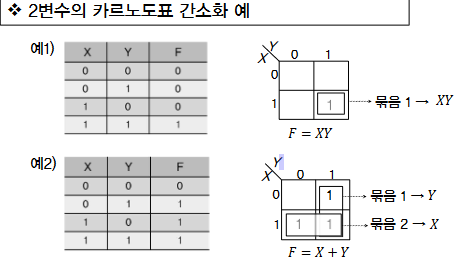
| 2변수 카르노 도표 | |
| 2 개의 변수를 가지는 부울함수 => 4개의 최소항 (4개의 정사각형으로 구성) | |
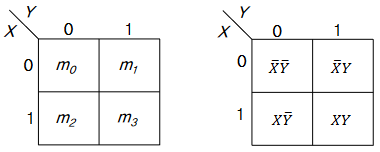 |
 |
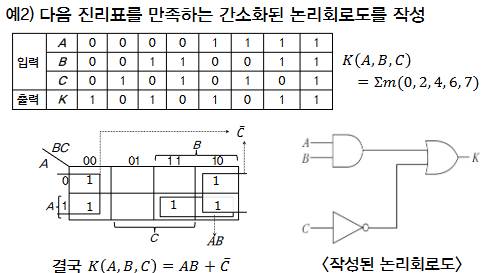
| 3변수 카르노 도표 | |
| 3 개의 변수를 가지는 부울함수 => 8개의 최소항 (8개의 정사각형으로 구성) | |
 |
 |
 |
 |
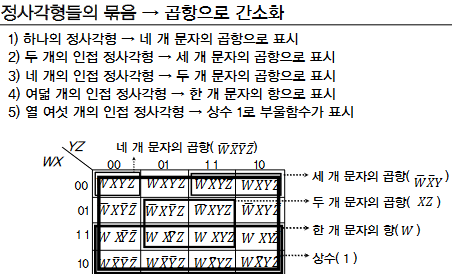
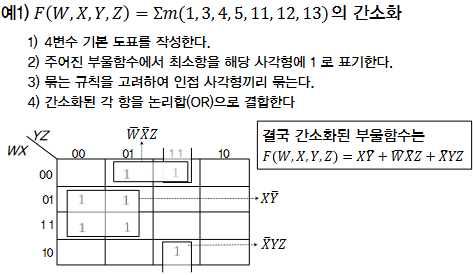
| 4변수 카르노 도표 | |
| 4 개의 변수를 가지는 부울함수 => 16개의 최소항 (16개의 정사각형으로 구성) | |
 |
 |
 |
 |
무관조건 (카르노 도표 : x 로 표현)
- 정의 : 입력변수들의 조합에 따라 함수값이 발생하지 않는 경우
- 함수값이 0과 1 중 어떤 출력값이 나와도 무관한 경우
- 부울함수를 더욱 간소화
BCD 코드의 경우
- 2진수 16개 조합 중 10개 조합만 사용
- 나머지 6개 조합(1010,1011,1100,1101,1110,1111)은 미사용 => 발생하지 않는다는 가정 (무관하게 동작)
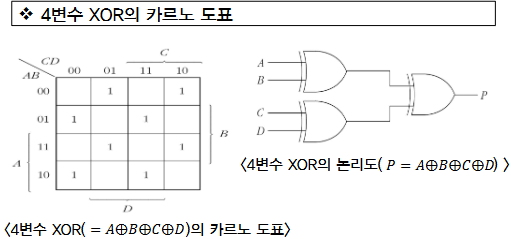
XOR의 카르노 도표
- 3변수 XOR 의 논리식
3변수 XOR : 한 변수가 1이거나 세 변수 모두 1인 경우
2변수 XOR : 오직 한 변수만 1인 경우
다중 변수 XOR(홀수함수) : 홀수개의 변수가 1
 |
 |
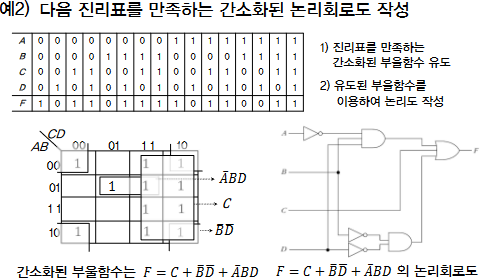
3. NAND와 NOR 게이트를 이용한 구현방법
- 실제 회로는 NAND와 NOR 게이트로 구현 (AND, OR 게이트에서 변환 필요)
- 전자회로로 제작이 용이 회로구성이 동일 게이트로 구성되는 것이 유리
| NAND 게이트만으로 연산 구현 | NAND 게이트의 그래픽 기호 | ||
 |
 |
||
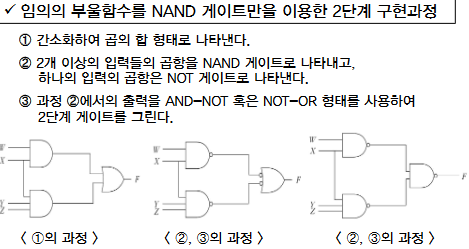
| 2단계 구현 | 다단계 구현 | ||
 |
 |
||
| NOR 게이트만으로 연산 구현 | NOR 게이트의 그래픽 기호 | ||
 |
 |
||
| 2단계 구현 | 다단계 구현 | ||
 |
 |
||
 |
정답 : 3 |
 |
정답 : 4 |
 |
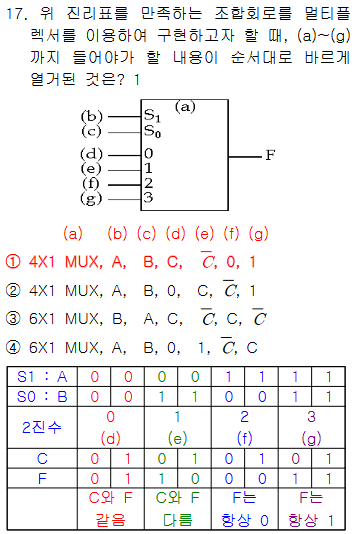
정답 : 2 |
 |
 |
 |
 |
'Self-Study > Study' 카테고리의 다른 글
| [디지털논리회로#9,10,11]순서논리회로 (0) | 2022.05.22 |
|---|---|
| [디지털논리회로#6,7,8]조합논리회로 (0) | 2022.05.21 |
| [디지털논리회로#2,3]논리게이트와 부울대수 (0) | 2022.05.21 |
| [디지털논리회로#1]디지털 논리회로와 데이터표현 (0) | 2022.05.21 |
| [데이터베이스시스템#11~14]해싱과 특수 인덱스 (0) | 2022.05.19 |




