New World
[이산수학#11] 트리 본문

1. 기본사항
트리 : 사이클이 없는 단순 연결 그래프
Trivial Tree : 꼭지점 하나로 구성된 트리
Empty Tree : 꼭지점이 하나도 없는 트리
Forest : 한 개 이상의 트리로 구성된 트리
루트 트리 : 루트라 부르는 노드가 존재하며 나머지 노드들이 서로 분리된 집합으로 나뉘는 트리
트리 -> 루트 트리 (서브트리, 루트 노드)
| 트리 | 노드 | 용어 |
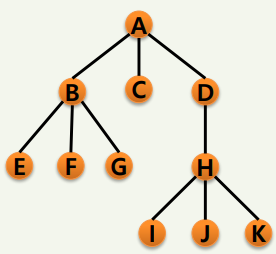 |
자식 노드 : A 기준으로 B, C, D A의 차수 : 자식 노드의 수 |
레벨 : 루트에서 어떤 노드까지의 경로의 길이 |
| 부모 노드 : B(C or D) 기준으로 A B(C or D) 의 차수 : max { B(C or D)의 차수 | 𝑵 ∈ 𝑻 } |
||
| 형제 노드 : B 기준으로 C, D | 높이(깊이) : max { N의 레벨 | 𝑵 ∈ 𝑻 } | |
| 리프 노드 : 단말 노드, C | ||
| 내부 노드 : 안에 있는 노드 B 기준으로 E, F, G H 기준으로 I, J, K |
무게 : 리프 노드들의 개수 |
| 트리의 표현 | |
| 중첩된 집합 |  |
| 중첩된 괄호 | (A (B (E) (F) (G)) (C) (D (H (I) (J) (K)))) |
| 결각 |  |
2. 이진 트리
공집합이거나 모든 노드가 최대 2개의 서브트리를 갖는 루트 노드인 트리

완전 이진 트리 : 왼쪽 노드부터 차례로 채워진 이진트리
- 같은 노드 수를 갖는 트리 중 최소 높이
-n개의 노드를 갖는 이진 트리의 최소 높이 : 𝑯𝒎𝒊𝒏 = |𝒍𝒐𝒈𝟐n|
포화 이진트리 : 모든 노드가 채워진 이진 트리
3. 이진 탐색 트리
정의 : 모든 노드가 탐색을 위한 키값을 가지며 왼쪽 서브트리의 키값들은 해당 키값보다 작아야 한다
검색:
1. 루트 노드로 설정

2. 주어진 키를 비교
-일치 : 키 반환, 탐색 멈추기
-노드보다 작으면 : 왼쪽 자식을 탐색 노드로 설정, 왼쪽이 없을 경우 키 없음을 반환하며 탐색 멈추기
-노드보다 크면 : 오른쪽 자식을 탐색 노드로 설정, 오른쪽이 없을 경우 키 없음을 반환하며 탐색 멈추기
3. 2번 과정을 반복
4. 트리의 활용
신장 트리 : 그래프의 모든 꼭지점을 포함하는 트리
최소 신장 트리 : 모든 변의 가중치 합을 총 가중치라 할 때, 가장 작은 신장 트리
Kruskal 알고리즘
1. 가중치의 오름차순으로 변을 정렬
2.가장 작은 변부터 차례대로 트리에 추가
3. 모든 꼭지점이 연결될 때까지 2반복
Prim 알고리즘
1. 꼭지점 하나를 트리에 추가
2. 트리와 연결된 꼭지점 중 가장 작은 가중치의 변으로 연결된 꼭지점을 추가
3. 2번 과정 반복
'Self-Study > Study' 카테고리의 다른 글
| [이산수학#13] 정수론 (0) | 2022.05.08 |
|---|---|
| [이산수학#12] 조합이론 (0) | 2022.05.08 |
| [이산수학#9,10] 그래프 (0) | 2022.05.06 |
| [이산수학#8] 부울대수 (0) | 2022.05.06 |
| [이산수학#7] 함수 (0) | 2022.05.06 |



